Let’s face it: frogs are not the most glamorous of animals…However, we owe a great deal to them! In 1780, Luigi Galvani found out that muscles of frog’s legs would twitch if in contact with electrical stimuli.
Today we know that this is due to one remarkable property of biological tissues: the fact that they can actively respond to electric signals. This is enabled by the presence of ions in the extracellular and intracellular compartments, and by the fact that cells in our body such as neurons and muscular cells have ion channels in their membranes that can control the flow of ions through it. The latter allow these cells to generate, propagate and transmit electrical oscillations of the membrane known as action potentials. Action potentials are the signals our brain uses to communicate…and compute! The electrical nature of these phenomena allows us to measure the electrical activity of certain organs with devices placed in contact with the skin, just as one would do to measure the voltage difference across a resistor in a high-school physics experiment!

Biosignal recording techniques like EEG and ECG take advantage of that. More intriguingly, we can use external current sources to alter the “normal” behavior of these cells. The latter generate an electric field (E-field) in the tissues which will affect the membrane potential of excitable cells. This is the case of non-invasive brain stimulation techniques such as transcranial current stimulation (tCS).

But what is this E-field we have been talking about so much? The E-field is a vector, i.e., a mathematical entity that has, in each point in space, a direction and a magnitude (in Volts per meter). In conductive materials (like the ones in our heads), it drives an electric current: the E-field exerts a force on charged ions establishing a current. The E-field generated during tCS is thought to interact mostly with pyramidal cells in the cortex. According to cable theory[1], which deals with the interaction between the E-field along a neuron and the changes in membrane potential it produces, an E-field directed along the pyramidal neuron and directed towards its soma will lead to an increase in soma excitability. The opposite happens when the E-field points from the soma to the apical dendrite. The fact that pyramidal cells tend to align perpendicularly to the cortical surface, suggests that the component of the E-field along this direction (En) is the most important one in predicting the effects of tCS[2].
The E-field established in the brain during tCS depends on multiple factors: the geometry of the electrodes and the currents injected through them, the geometry of the head and the electrical properties of the tissues (like the electrical conductivity, i.e., a measure of how well a tissue conducts electric current)[3]. The physics equations that allow us to calculate the E-field in the head, assuming we have knowledge about the previously listed parameters, are well studied and have been known for years from electromagnetism[4]. However, only recently has it become possible to numerical solve these equations in a manner of hours, due to the available powerful computational resources!
The creation of a head model suitable for E-field calculations is usually based on MRI structural images. The latter are segmented into the different tissues comprising it. Usually models include scalp, skull (in some cases this is segmented into compact and spongy bone), cerebrospinal fluid (CSF), grey-matter (GM) and white-matter (WM). 3D surfaces of these tissues are then calculated based on the segmented masks. At this stage electrode models are also represented on the surface of the scalp.
The finite element (FE) method is normally used to numerically solve the equations and calculate the E-field in the head. In this method, the geometry of the head is discretized into simpler geometric shapes (finite elements). This geometric discretization is called the finite element mesh. A full explanation of the FE method is beyond the scope of this blog, but a (very) mathematically inclined reader can read more details in [5]. The FE method allows for the efficient and accurate calculation of an approximation to the E-field in each vertex of the FE mesh (nodes of the mesh).

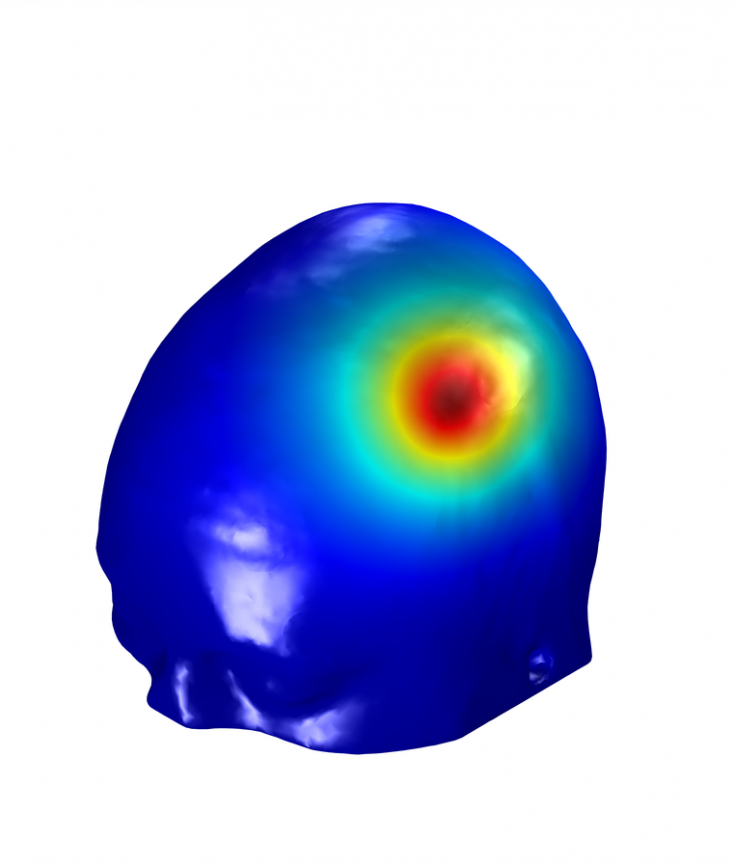
After all this work, the brave researcher that has successfully created a head model is rewarded with a powerful tool that can, for example, be used as a complementary analysis to the results of an experiment using a specific montage to stimulate a group of subjects. These models can be created on a subject by subject basis, thus allowing for analysis of average En-field values in some regions of interest in the brain. A more interesting approach is to use these models during experimental design, to determine the montage that better targets a specific region (or a network of regions) in the brain[6]. In NE’s Stimweaver implementation of this montage optimization the target is defined based on the type of desired effect (increase in excitability, decrease in excitability or no-change) and on the weight with which that effect should be enforced during the optimization. The algorithm[2] then determines the optimized montage constrained by maximum number of electrodes, maximum total injected current and maximum current per electrodes.

In the eternal words of George Box, “(…) all models are wrong (…)” since all models make assumptions and simplifications of reality. However, we can ask ourselves: “Is the model illuminating and useful?”. The type of head models we have described in this blog entry have proven (and continue to do so) their usefulness in analyzing the E-field distribution in commonly used montages and in planning experiments. If you can look past an admittedly steep (at first) learning curve, you will be rewarded with a powerful tool that can really help your experiment reach the next level in terms of results…In any case our team at NE is always available to help you create these models and take full advantage of them!
Useful resources:
NIC software: Did you know you can use NIC to visualize the E-field distribution in any montage with PiStim electrodes? And you can do it in two available head models (one male and one female). We are always updating NIC so stay tuned for more features!
Stimweaver service: We perform optimization of montages in a standard head model with a target map that you can create here! We can also map more complex target maps to this subject or run optimizations based on personalized head models. For more information contact us.
References:
[1] Roth BJ. Mechanisms for Electrical-Stimulation of Excitable Tissue. Critical reviews in biomedical engineering. 1994;22(3-4):253-305.
[2] Ruffini G, Fox MD, Ripolles O, Miranda PC, Pascual-Leone A. Optimization of multifocal transcranial current stimulation for weighted cortical pattern targeting from realistic modeling of electric fields. NeuroImage. 2014;89:216-25.
[3] Miranda PC, Mekonnen A, Salvador R, Ruffini G. The electric field in the cortex during transcranial current stimulation. NeuroImage. 2013;70:48-58.
[4] Rush S, Driscoll DA. Eeg Electrode Sensitivity – an Application of Reciprocity. IEEE Trans Biomed End. 1969;Bm16(1):15-&.
[5] Johnson CR. Computational and numerical methods for bioelectric field problems. Critical reviews in biomedical engineering. 1997;25(1):1-81.
[6] Fischer DB, Fried PJ, Ruffini G, Ripolles O, Salvador R, Banus J, et al. Multifocal tDCS targeting the resting state motor network increases cortical excitability beyond traditional tDCS targeting unilateral motor cortex. NeuroImage. 2017;157:34-44.