Electrical recordings from the brain, obtained through techniques like Stereotactic-electroencephalography (SEEG) and scalp EEG, offer invaluable insights into the brain’s functioning. Paired with mathematical models, they can boost our understanding of brain processes, as well as aid the research on pathologies such as epilepsy and the design of optimal therapeutic strategies. Yet, relating the physics of the electrophysiological recordings with those mathematical models remains a challenge. To address this challenge we need to first understand the origin of the electrical signals that can be measured.
The origin of the electrophysiological recordings
The electric potentials in the low frequency range (below a few kHz) that can be recorded by extracellular electrodes are generated by the transmembrane currents induced by synaptic inputs onto the neurons (postsynaptic currents). An excitatory synaptic input produces an inward current that is seen as a negative current source (i.e. a sink) from the extracellular medium.
Conversely, an inhibitory synapse causes an outward current that is seen as a positive current source (i.e. a source) from the outside. Within the typical measurement timescales, these current sinks or sources are always balanced by a passive return current to achieve electroneutrality. The synaptic currents and their associated return currents give rise to a current source distribution in the brain. If, in a brain region, many of such currents synchronize in time and with a coherent spatial distribution, then a measurable voltage perturbation is produced.
This is more easily achieved by the pyramidal cells due to the elongated shape of their dendritic trees and their preferential orientation perpendicular to the cortical surface.
Mesoscale models of neural activity using NMMs
A common approach to build meso scale models of brain activity is the use of neural mass models (NMMs). NMMs are mathematical representations of the collective behavior of neurons in the brain. They provide a way to capture the interactions and dynamics of large populations of neurons by considering their average behavior within brain regions (i.e. cortical patches).
NMMs can provide valuable insights into the overall electrical patterns and dynamics of brain function and have been used to simulate electrophysiological recordings such as EEG or stereotactic-EEG (SEEG).
NMMs are a mathematical abstraction, but the variables that describe the dynamics in these models can be used as a starting point for a physical model. The raw outputs of NMMs are the mean synaptic activity, membrane potential alteration, and firing rates of each of the populations involved. In fact, the membrane potential of the pyramidal cell populations taken directly from NMMs is commonly used as a proxy for EEG or SEEG recordings.
This implies assuming that the membrane potential is proportional to the voltage measured by the recording electrodes. Which from a physics viewpoint is not realistic.
A journey through multiple scales
In a recent paper by our team published in the Journal of Neural Engineering, we proposed a framework to link NMM formalism and physical models of electrophysiological recordings. The framework is based on a multi-scale modeling approach with the story beginning at the single-cell level (See Figure 1 below).
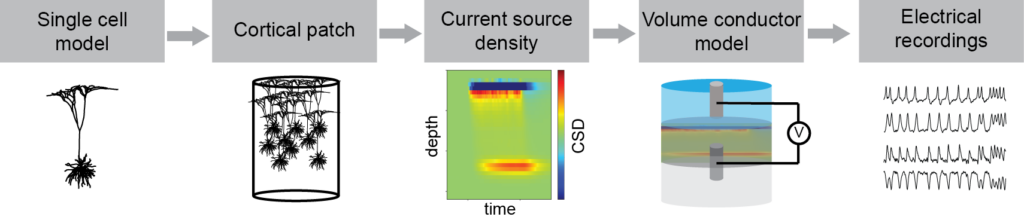
By using reconstructed morphologies of pyramidal cells we built highly detailed electrical models and used them to simulate the currents flowing through the cell membrane as a response to a synaptic input. We combined a large number of these models and placed them inside a small cylinder to represent a cortical patch. By doing so, we could calculate the overall current source density (CSD) that is generated inside a patch when a specific type of synaptic input happens in many cells at the same time (e.g. inputs in a certain cortical layer). Once the CSD is obtained, we are no longer at the microscale level and we have moved to the mesoscale instead.
We used this approach to generate the CSD as a result of synaptic inputs onto each of the cortical layers. Since currents and voltages follow the superposition principle, these results can be used to obtain the equivalent CSD of any combination of synaptic inputs at the cortical layers over time. To do so, at any point in time, we can simply calculate the total CSD as a linear combination of the inputs into each of the cortical layers (using the aforementioned results).
Finally, the CSD of a cortical patch (or many of them) can be used, together with a suitable volume conduction model, to simulate any type of electrical recordings. Thus, moving to the macroscale world and finishing our journey through scales.
Bridging the gap between NMMs and physical models
One of the raw outputs that can be obtained from NMMs is the post-synaptic membrane perturbations associated with each of the neural populations. If we assume that these perturbations are proportional to their associated post-synaptic currents we can make a link between NMMs and the physical models. For that, we need to define the locations of the synaptic contacts (distribution over the cortical layers) and after that, we can use the results described in the previous section to calculate the CSD over time generated by the neural activity.
Although the locations of the synaptic contacts are not explicitly defined in NMMs, every population in these models represents one or more cell types. Thus, it is possible to estimate the distribution of every synapse across the layers from the literature. In fact, in our study, we presented an example as a proof of concept of the use of the proposed framework.
The example consists of a very simple Jansen-Rit model, for which we defined a synapse distribution for each pre-synaptic population going into the principal cell population based on the literature (see Figure 2 below). We used this model to simulate the CSD inside a cortical patch generated by the model’s activity.
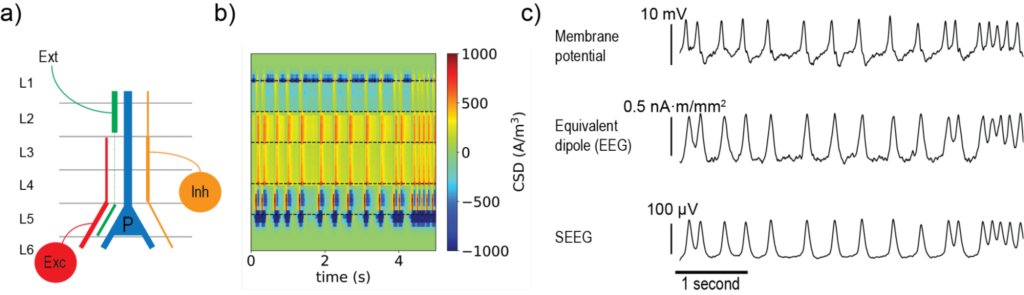
Figure 2b displays the CSD over time as a function of depth. Given that sinks and sources can originate either from a synaptic input or by their associated return currents, even in such a simple scenario the interpretation of the currents in the different layers are quite ambiguous.
From CSD to electrophysiological recordings
We then used the simulated CSD to calculate the equivalent dipole strength over time (the signal that would be “seen” by a scalp EEG electrode from this cortical patch). The same distribution was also used to simulate a bipolar SEEG recording inside the cortical patch. These results, together with the membrane potential over time at the principal cell population are shown in Figure 2c. It is very interesting to note how the membrane potential from the NMM, the dipole moment, and the SEEG signal, despite showing the same patterns, all look slightly different. This highlights the importance of using the right physical models when simulating electrophysiological recordings.
