In a previous post, I explained the basic steps in EEG data analysis. Now I will go trough the type of EEG features most commonly used in EEG applications.
First of all, we have to understand that an EEG signal is a discrete time series (or a set of discrete time series if we consider more than one channel), and thus all discrete signal processing techniques can be applied here. The research field of discrete signal processing techniques is huge and fascinating and it can get very complex. For now I will provide a classification of different types of EEG features, along with some examples.
Time domain features:
From a time series we can extract a lot of statistical information such as the mean and the standard deviation. We can even go a step beyond and compute a histogram, i.e. the distribution of my data sample. From here we can compute the kurtosis(peakedness of my distribution compared to a Gaussian distribution) and theskewness (the degree of asymmetry of my distribution compared to a Gaussian one).
In addition to those somehow simple and intuitive statistical features we can extract advanced features such as the fractal dimension (i.e. Hurst Exponent) related with the long term memory of a time series or the Entropy which quantifies the amount of regularity and the unpredictability of fluctuations over our time series.
More advanced techniques include Detrended fluctuation analysis, which is similar to the computation of the Hurst Exponent, but in this case it can be applied to non-stationary signals.
Another interesting approach is the Visibility Graph, a smart method to convert a time series into a graph. Once we have our graph, we can apply complex network techniques to extract information from our original time series.

Frequency domain features:
Since around 1822, when Joseph Fourier presented his work on Heat Flow, we know that any time series can be represented by an infinite sum of sines functions. In other words, we can transform any time signal to his frequency domain in which we can see the different frequencies that compose our original time series.
This mathematical breakthrough has been very used since then and it has had strong implications in EEG data analysis. Since the discovery of alpha waves by Hans Bergerin 1924, we know that EEG can be seen as a mixture of signals with different frequencies. The study of these EEG frequencies has been going on since then.
In particular, some BCIs rely on this principle. If I detect a particular frequency in a particular area of the brain, the BCI will interpret the user’s intention to move right, for instance.
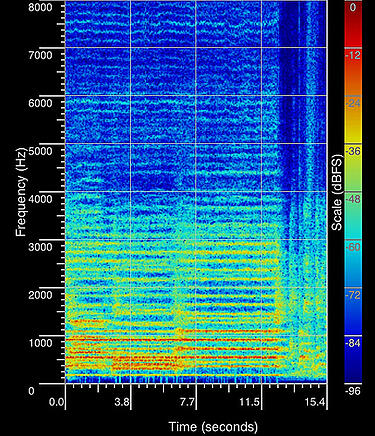
We can also represent our EEG data in a spectrogram, where we can see the evolution of the frequencies over time. It is somehow a compromise between the time and frequency representation.
Finally, we can also include wavelets analysis to this section. It is a very powerful technique for digital signal processing and has been widely used in several fields.
Synchronicity features:
In this type of features what we do is to study the relationship between two or more time series. In our EEG case, each time series would represent a different channel. Some synchronicity features includes correlation, mutual information, coherence and synchronisation likelihood, just to mention a few.
More complex approaches can be done, such as the one explained in this previouspost, in which a 64 node graph is generated from an EEG recording of 64 channels.
As mentioned, the field of signal processing and feature extraction techniques is very broad and my objective here was just to give a brief overview, focusing more onEEG features. A full report of all the features used nowadays in EEG would be unpractical in a short post as this one, but I hope at least to bring some inspiration forEEG data researchers. Any comments are more than welcome. See you soon!