Broadly speaking, when we talk about analysing EEG signals, we are talking about how to use those time-varying signals to classify clinical conditions, behavioural events or predict responses (is the person awake or not? is this person going to develop Parkinson?). As such, learning temporal dependencies in those time series and predicting or classifying events with that is an essential step on the study of EEG signals.
But wait, isn’t that one of the main function of our brain? Our neurons, embedded in networks, continuously process time-varying sensory information and, through integrating and learning temporal dependencies in those signals, they are able to perform classification and prediction, ensuring our own survival (Friston and Kiebel 2009). So, what can we learn from our own cortical networks for the analysis of EEG signals?
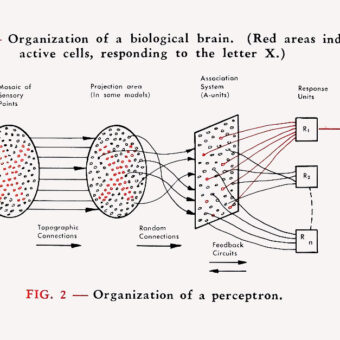
Neurons in the brain are wired with an abundance of recurrent and feedback connections. Those structures, that continuously process sensory information, are able to integrate, remember and manipulate to produce an output function or behaviour. How can that occur? The presence of the recurrent and feedback structures, together with slow plasticity mechanisms that are intrinsic of those neurons, allow the cortical network to remember past stimuli. The presence of large populations of neurons that perform a non-linear transform of their stimulus (the generation of an action potential) act as a reservoir to integrate and manipulate stimulus information. With this organization in mind, the learning of temporal dependencies for prediction and classification can be achieved by the training of a simple linear readout that observes the network activity (see Figure).
This approach is known as the reservoir-computing framework (Buonomano and Maass 2009). In essence, the theory states that systems of recurrently connected non-linear dynamical units (with decaying memory traces) are able to perform history-dependent computations on time-varying stimuli, which are decoded from the activity itself by readout units. Interestingly, the generality of this framework is exemplified by recent advancements where the cortical and recurrent network has been replaced by a single delayed-non-linear differential equation (or a laser, see Appeltant et al., 2011), a bacterial cell culture (Jones et al. 2007) or a soft-silicon body (Nakajima et al. 2015).
And now, imagine we set-up our EEG experiments (properly designed, see our post on ‘5 basic Guidelines to Carry Out a Proper EEG Rerecording Experiment’) and collect a set of time-series associated to diverse clinical or behavioural conditions. Could we have a cortical network model processing those signal and performing the prediction or classification of those conditions that we are interested on? Yes. And there are, actually, few studies that have applied this framework for the analysis of the EEG and the classification/prediction of clinical or behavioural conditions. For instance, Buteneers et al. 2013 successfully predicted epileptic seizures from intracranial EEG, with an average detection delay of 1 sec, outperforming other state-of-the art algorithms used in clinical settings, with a sensitivity and specificity above 95%. Similarly, Schleibs et al. 2013, achieved a classification accuracy of 82% when analysing EEG recorded in relaxing state and memory task. So far, promising!
But one of the most interesting things regarding the reservoir-computing framework is that, as the reservoir is a dynamical system, the analysis of its dynamics can be performed in real time too. In other words, the performance of classification/prediction performed by the readouts can be evaluated in continuous time as the EEG data arrives the system (see Lukoševičius and Jaeger 2009 for a review on readout algorithms). This could have tremendous implications for brain-computer interface (BCI) approaches (and brain to brain (BtB) approaches!), which essentially rely on the efficiency of the algorithms performing the closed-loop information transfer between computers and brains.
Another relevant aspect is that with this approach, there is no need to explicitly indicate what features of the EEG we may be interested in (is there a power modulation at a particular frequency? coherence?). The prediction/classification of stimuli can be performed on the network responses arising from the EEG signals, which are automatically transformed to a higher dimensional space by the non-linear nodes of the reservoir. However, this can also be seen as a drawback from the pure neuroscientific curiosity: if there is no explicit knowledge of what are the particular features on your signals that allow performing such prediction or classification, how can I understand the mechanism? So far, the algorithm can only be used as black box that internally creates and selects the best features, especially when some learning process is added on the network.
When introducing the learning, we are bringing in another critical aspect of this approach: the number of parameters involved on the algorithm is rather high, and its parametrization is necessary to ensure stability of the system (Verstraeten and Schrauwen, 2009). While such discussion is reminiscent from the artificial neural network community, recent studies propose the use of biologically-based synaptic plasticity mechanisms as self-organizing rules that ensure stability of the network (Lazar et al., 2007, Castellano 2014).
Putting together all we have seen, the usage of biologicaly-based cortical networks as algorithms for the analysis of EEG data seems promising, especially where the implementation allows for the real-time analysis of data. Could we learn from it and improve clinical prediction or classification algorithms? Keep posted! If you have any question regarding this post, or you want to learn more about learning algorithms, please do not hesitate to send us a message (also, very interesting presentations can be found here and here).
__
Appeltant, L., Soriano, M. C., Van der Sande, G., Danckaert, J., Massar, S., Dambre, J., … Fischer, I. (2011). Information processing using a single dynamical node as complex system. Nature Communications, 2, 468.
Buonomano, D. V, & Maass, W. (2009). State-dependent computations: spatiotemporal processing in cortical networks. Nature Reviews Neuroscience, 10, 113–125.
Castellano, M. (2014). Computational Principles of Neural Processing : modulating neural systems through temporally structured stimuli (PhD thesis, chapter 2).
Friston, K., & Kiebel, S. (2009). Predictive coding under the free-energy principle. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 364(1521), 1211–1221.
Jones, B., Stekelo, D., Rowe, J., & Is, C. F. (2007). Is there a liquid state machine in the bacterium escherichia coli? IEEE Artificial Life.
Lazar, A., Pipa, G., & Triesch, J. (2009). SORN: a self-organizing recurrent neural network. Frontiers in Computational Neuroscience, 3(October), 23.
Lukoševičius, M., & Jaeger, H. (2009). Reservoir computing approaches to recurrent neural network training. Computer Science Review, 3(3), 127–149.
Nakajima, K., Hauser, H., Li, T., & Pfeifer, R. (2015). Information processing via physical soft body. Scientific Reports, 5, 10487. http://doi.org/10.1038/srep10487
Schliebs, Stefan, Elisa Capecci, and Nikola Kasabov. “Spiking Neural Network for On-line Cognitive Activity Classification Based on EEG Data.” Neural Information Processing. Springer Berlin Heidelberg, 2013.
Verstraeten, D., & Schrauwen, B. (2009). On the Quantification of Dynamics in Reservoir Computing. Lecture Notes in Computer Science, 985–994.